最新：Iterative Random Forestが高次の交互作用を抽出できる期待のアルゴリズムか

機械学習は基本的に、入力と出力の間の関数が一切未知であるとした前提で、その謎の関数と同等の精度で結果を出せる関数をデータから見出すのが仕事です。なので基本的には統計と違って確率分布や線形性、どの変数間が交互作用を持つかなどは一切仮定しないです。

大前提、機械学習の哲学としては、「全ての情報は有益かもしれないという立場の元、最大限に予測精度を高める」ことを信条にしています。なので、予測精度がどれだけ高いか、というのが肝だったり。とはいえ、ブラックボックスを作るだけでは解釈までは難しい、せめてどの変数がどう出力に影響するのか？というのはある程度把握したいわけです。

で、よく言われるのが、機械学習は変数間の交互作用（Interaction）も勝手に見つけて考慮してくれるから強い、というやつです。特に、非線形で高次の交互作用（Nonlinear higher-order variable interaction）を上手くキャプチャーしてくれる、というやつ。たしかに、おそらく理論的にはそのような複雑な変数間の関係性を掴んでくれていたりするはず、ブラックボックスの中で。

しかしながら、「機械学習で高次の交互作用を捉えているというけど、じゃあどの変数がどういう風に関係しあっているの？」という質問に答えるすべがほとんどなかったりします。一応それっぽいアルゴリズムはいくつか提唱されているけど、大抵のものはいまいちな感じ。。そこでついに出てきた期待の（現時点おそらく最強）アルゴリズムが、BasuらによるiRFというやつです。

 Basu et al. (2018) Iterative random forests to discover predictive and stable high-order interactions. PNAS 

Iterative random forests to discover predictive and stable high-order interactions | PNAS

2017年にはすでにArxivに投稿されていて、強い興味を持っていたのですが、PNASに出てくるとは・・。

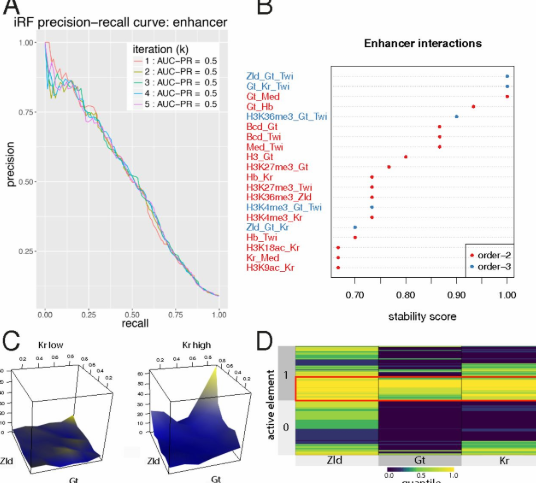
これは、Random forestをベースにしていて、論文の事例では２次・３次・４次・５次・６次の交互作用を総当たりで評価して、どれが一番大事かを評価してみたりしています(上の図では３次までだけど、論文中には６次とか平気で出てきます)。面白いのは、例えば２次の交互作用（A*B）が重要でなくとも、３次（A*B*C）が大事だったりすること。こんなん、事前に式を立てるパラメトリックな統計では決して思いつけないですよね。このアルゴリズムを使うと、どの変数らを一緒に考えないといけないのか、というのが容易に抽出できるようになるかもしれません。

なお、Rで既にパッケージ化されているので、試してみたくもある。